初中数学
简答题案例:某习题课上,老师让学生独立完成如下例题。
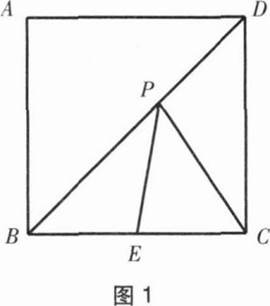
如图1,在边长为3的正方形中,E是BC的中点,P是BD上的动点,当BP为何值时,PE+PC的值最小?
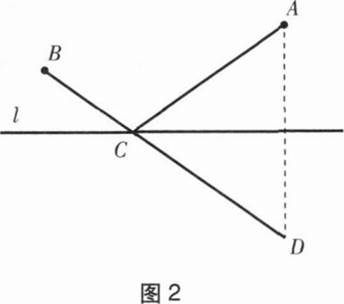
大多数学生表示不会做,教师这样启发:回顾以前学过的“饮马问题”,如图2,牧马人从A地出发,到一条笔直的河边ι饮马,然后回到B地,牧马人到河边什么地方饮马,所走的路径最短?
作点A关于直线ι的对称点D,连接BD,交直线ι于点C。由于AC+BC=BC+CD=BD,利用两点之间线段最短,此时点C使AC+BC最小,点C即为所求。你能用这种方法解决上面的问题吗?
学生:哦,会做了……
问题:
(1)给出该例题的求解过程;(10分)
(2)指出该教师对学生的启发有哪些合理和不足之处。(10分)
如图1,在边长为3的正方形中,E是BC的中点,P是BD上的动点,当BP为何值时,PE+PC的值最小?
大多数学生表示不会做,教师这样启发:回顾以前学过的“饮马问题”,如图2,牧马人从A地出发,到一条笔直的河边ι饮马,然后回到B地,牧马人到河边什么地方饮马,所走的路径最短?
作点A关于直线ι的对称点D,连接BD,交直线ι于点C。由于AC+BC=BC+CD=BD,利用两点之间线段最短,此时点C使AC+BC最小,点C即为所求。你能用这种方法解决上面的问题吗?
学生:哦,会做了……


问题:
(1)给出该例题的求解过程;(10分)
(2)指出该教师对学生的启发有哪些合理和不足之处。(10分)
参考答案:暂无进入在线模考
(1)下面给出两种求解方法。

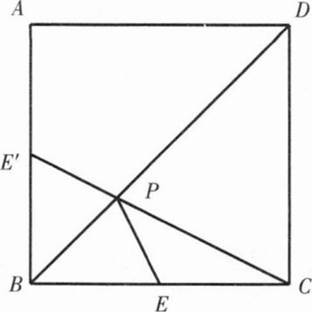
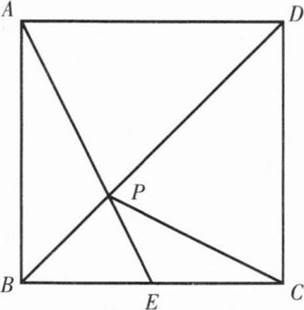
(解法二)在正方形中,顶点A,C关于对角线对称,连接AE交BD于点P,则AP=CP,所以有PE+PC=PE+AP=AE,根据两点之间线段最短,AE即为PE+PC的最小值。

(2)合理之处:①运用以前学过的“饮马问题”启发,说明教师能够以学生已有的知识、经验为基础,引导学生思考,促进学生巩固基本的数学知识与技能;②将本节课需解决的习题中的核心问题,转化为更简单的“饮马问题”,体现了转化思想方法的运用,让学生经历由易到难解决问题的过程,获得基本的数学活动经验。
不足之处:教学活动是师生积极参与、交往互动、共同发展的过程,学生是学习的主体,教师是学习的组织者、引导者与合作者,案例中教师在启发过程中更侧重于讲解,缺乏引导学生自主思考,使教学活动的有效性受到限制,启发的目的大打折扣。


(解法二)在正方形中,顶点A,C关于对角线对称,连接AE交BD于点P,则AP=CP,所以有PE+PC=PE+AP=AE,根据两点之间线段最短,AE即为PE+PC的最小值。


(2)合理之处:①运用以前学过的“饮马问题”启发,说明教师能够以学生已有的知识、经验为基础,引导学生思考,促进学生巩固基本的数学知识与技能;②将本节课需解决的习题中的核心问题,转化为更简单的“饮马问题”,体现了转化思想方法的运用,让学生经历由易到难解决问题的过程,获得基本的数学活动经验。
不足之处:教学活动是师生积极参与、交往互动、共同发展的过程,学生是学习的主体,教师是学习的组织者、引导者与合作者,案例中教师在启发过程中更侧重于讲解,缺乏引导学生自主思考,使教学活动的有效性受到限制,启发的目的大打折扣。
你可能感兴趣的试题
最新试题
下面是某教材“平行四边形”一章中“菱形”一节的主要内容。我们观察平行四边形的一组邻边,如图18.2-6, 当这
类型:简答题2023-03-12
案例:学生学习了“一次函数”后,李老师布置了一个家庭作业:提出一个关于“一次函数“的实际问题并加以解决, 下面是小颖完成
类型:简答题2023-03-12
阐述中学数学课程中统计与概率的联系,以及二者在研究对象、总体分布、 结果评判三个方面的区别。
类型:简答题2023-03-12
袋子中有5张卡片,分别写有数字1- 5, 从袋中随机抽取一张卡片,记卡片上的数字为b。 放回袋中,再
类型:简答题2023-03-12
简述在中学数学教学中确定教学目标的主要依据。
类型:简答题2023-03-12
请回答义务教育数学课程中"数感"的含义,并举例加以解释。
类型:简答题2023-03-12
类型:简答题2023-03-12
类型:简答题2023-03-12
类型:简答题2023-03-12
义务教育阶级数学命题的主要类型包括( )。
类型:单选题2023-03-12


