初中数学
简答题材料:
下面是初一下学期教材“平行线的判定”的部分内容。
根据平行线的定义,如果平面内的两条直线不相交,就可以判断这两条直线平行。但是,由于直线无限延伸,检验它们是否相交有困难,所以难以直接根据定义来判断两条直线是否平行。那么,有没有其他判定方法呢?
思考
我们以前学过用直尺和三角尺画平行线(图1)。在这一过程中,三角尺起着什么样的作用?
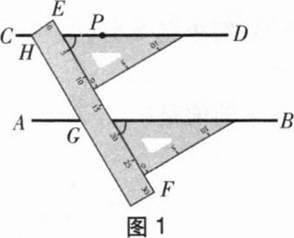
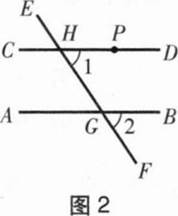
简化图1得到图2。可以看出,画直线AB的平行线CD,实际上就是过点P画与∠2相等的∠1,而∠2和∠1正是直线AB,CD被直线EF截得的同位角。这说明,如果同位角相等,那么AB//CD。
一般地,有如下利用同位角判定两条直线平行的方法:
判定方法1两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单说成:同位角相等,两直线平行。
根据上面的内容,完成下列任务:
(1)说出其他判定方法,并使用判定方法l证明;(8分)
(2)写出这部分内容的教学设计,包含教学目标、重难点、教学过程(含指导教学的活动及设计意图)。(22分)
下面是初一下学期教材“平行线的判定”的部分内容。
根据平行线的定义,如果平面内的两条直线不相交,就可以判断这两条直线平行。但是,由于直线无限延伸,检验它们是否相交有困难,所以难以直接根据定义来判断两条直线是否平行。那么,有没有其他判定方法呢?
思考
我们以前学过用直尺和三角尺画平行线(图1)。在这一过程中,三角尺起着什么样的作用?

简化图1得到图2。可以看出,画直线AB的平行线CD,实际上就是过点P画与∠2相等的∠1,而∠2和∠1正是直线AB,CD被直线EF截得的同位角。这说明,如果同位角相等,那么AB//CD。
一般地,有如下利用同位角判定两条直线平行的方法:
判定方法1两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单说成:同位角相等,两直线平行。

根据上面的内容,完成下列任务:
(1)说出其他判定方法,并使用判定方法l证明;(8分)
(2)写出这部分内容的教学设计,包含教学目标、重难点、教学过程(含指导教学的活动及设计意图)。(22分)
参考答案:暂无进入在线模考
(1)判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
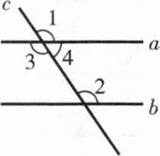
证明:如图,已知∠2=∠3,因为∠3=∠1,所以∠1=∠2,从而a∥b(同位角相等,两直线平行)。
判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
证明:如图,已知∠4+∠2=180°,因为∠4+∠1=180°,所以∠1=∠2,从而a∥b(同位角相等,两直线平行)。
(2)教学目标
知识与技能目标:掌握平行线的判定方法1,能够应用判定方法判断两条直线是否平行;
过程与方法目标:经历动手操作画出平行线的过程,发展探究意识,提升合情推理和演绎推理能力;情感态度与价值观目标:在活动中体验探索、交流、成功的乐趣,养成勇于探索、独立思考、大胆猜测的精神。
教学重难点
教学重点:掌握平行线的判定方法1。
教学难点:运用平行线的判定定理进行简单的推理证明。
教学过程
一、复习旧知
1.教师出示下图,通过提问的方式带领学生复习同位角、内错角、同旁内角的知识。
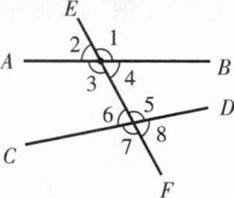
2.简单回顾平行线的相关知识。
【设计意图】以本节课的内容为中心,帮助学生梳理回忆学过的相关知识,为探索新知的顺利展开打好基础。
二、探究新知
1.提出探究问题
教师展示图片,提问学生若想知道图中木板的对边是否平行.应该怎样做。
2.动手操作
教师指导学生用三角尺和直尺画平行线,并提出思考问题:
(1)在画平行线的过程中,三角尺起着什么作用?
(2)由此能得出什么结论?
教师板书演示三角尺沿直尺移动的过程.使学生明确三角尺的作用是在画平行线的过程中,保证同位角相等,由此得出初步结论:同位角相等,两直线平行。
继续探究:当同位角不相等时,两直线可能平行吗?
教师通过多媒体演示直线的运动过程,使学生充分观察。引导学生得出结论:当同位角不相等时,两条直线不可能平行。
3.命题明确
判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
给出示意图,让学生尝试用数学语言描述该定理。
【设计意图】通过学生动手操作、多媒体演示等活动使学生发现平行线的判定方法,感受由特殊到一般的思想方法,初步培养合情推理能力。
三、课堂练习
1.如图,已知∠2=120°,∠4=60°,判断直线a与b是否平行?
2.如图,已知∠2=∠3,那么a与b平行吗?如果平行,请尝试证明。
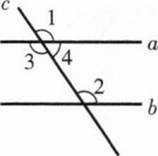
【设计意图】通过两道变式习题,巩固本节课所学知识的同时,也为学习平行线的另外两个判定方法作铺垫。
四、小结作业
小结:本节课你学>-2了哪些内容?有哪些收获和体会?
作业:思考是否还有其他方法可以判定两条直线平行。
【设计意图】课堂小结不仅能检验学生的学习情况,还能培养学生的语言表达能力;思考作业能够发挥学生学习的自主性,养成勤于思考、勇于探究的习惯。
证明:如图,已知∠2=∠3,因为∠3=∠1,所以∠1=∠2,从而a∥b(同位角相等,两直线平行)。
判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
证明:如图,已知∠4+∠2=180°,因为∠4+∠1=180°,所以∠1=∠2,从而a∥b(同位角相等,两直线平行)。

(2)教学目标
知识与技能目标:掌握平行线的判定方法1,能够应用判定方法判断两条直线是否平行;
过程与方法目标:经历动手操作画出平行线的过程,发展探究意识,提升合情推理和演绎推理能力;情感态度与价值观目标:在活动中体验探索、交流、成功的乐趣,养成勇于探索、独立思考、大胆猜测的精神。
教学重难点
教学重点:掌握平行线的判定方法1。
教学难点:运用平行线的判定定理进行简单的推理证明。
教学过程
一、复习旧知
1.教师出示下图,通过提问的方式带领学生复习同位角、内错角、同旁内角的知识。

2.简单回顾平行线的相关知识。
【设计意图】以本节课的内容为中心,帮助学生梳理回忆学过的相关知识,为探索新知的顺利展开打好基础。
二、探究新知
1.提出探究问题
教师展示图片,提问学生若想知道图中木板的对边是否平行.应该怎样做。
2.动手操作
教师指导学生用三角尺和直尺画平行线,并提出思考问题:
(1)在画平行线的过程中,三角尺起着什么作用?
(2)由此能得出什么结论?
教师板书演示三角尺沿直尺移动的过程.使学生明确三角尺的作用是在画平行线的过程中,保证同位角相等,由此得出初步结论:同位角相等,两直线平行。
继续探究:当同位角不相等时,两直线可能平行吗?
教师通过多媒体演示直线的运动过程,使学生充分观察。引导学生得出结论:当同位角不相等时,两条直线不可能平行。
3.命题明确
判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
给出示意图,让学生尝试用数学语言描述该定理。
【设计意图】通过学生动手操作、多媒体演示等活动使学生发现平行线的判定方法,感受由特殊到一般的思想方法,初步培养合情推理能力。
三、课堂练习
1.如图,已知∠2=120°,∠4=60°,判断直线a与b是否平行?
2.如图,已知∠2=∠3,那么a与b平行吗?如果平行,请尝试证明。

【设计意图】通过两道变式习题,巩固本节课所学知识的同时,也为学习平行线的另外两个判定方法作铺垫。
四、小结作业
小结:本节课你学>-2了哪些内容?有哪些收获和体会?
作业:思考是否还有其他方法可以判定两条直线平行。
【设计意图】课堂小结不仅能检验学生的学习情况,还能培养学生的语言表达能力;思考作业能够发挥学生学习的自主性,养成勤于思考、勇于探究的习惯。
最新试题
下面是某教材“平行四边形”一章中“菱形”一节的主要内容。我们观察平行四边形的一组邻边,如图18.2-6, 当这
类型:简答题2023-03-12
案例:学生学习了“一次函数”后,李老师布置了一个家庭作业:提出一个关于“一次函数“的实际问题并加以解决, 下面是小颖完成
类型:简答题2023-03-12
阐述中学数学课程中统计与概率的联系,以及二者在研究对象、总体分布、 结果评判三个方面的区别。
类型:简答题2023-03-12
袋子中有5张卡片,分别写有数字1- 5, 从袋中随机抽取一张卡片,记卡片上的数字为b。 放回袋中,再
类型:简答题2023-03-12
简述在中学数学教学中确定教学目标的主要依据。
类型:简答题2023-03-12
请回答义务教育数学课程中"数感"的含义,并举例加以解释。
类型:简答题2023-03-12
类型:简答题2023-03-12
类型:简答题2023-03-12
类型:简答题2023-03-12
义务教育阶级数学命题的主要类型包括( )。
类型:单选题2023-03-12