中学数学
①进-步理解角平分线的性质;
②能够灵活地运用角平分线的性质来解决数学问题;
③会运用角平分线尺规作图法解决实际问题。
他的教学过程设计中包含了下面的两道例题。
例题l:如图1,AC=BC,∠ACB=900,AD平分∠CAB,求证:AC+CD=AB。
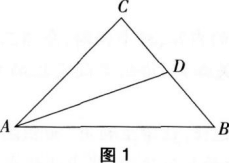
例题2:如图2,规划在城市A,B,C之间的三角区M建设-个物流中转中心,使它到公路AB,AC,BC的距离相等,试画图求出物流中心的建设位置。
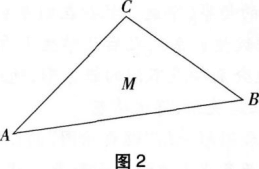
针对上述材料,完成下列任务:
(1)结合该教师的教学目标,分析例题1和例题2的设计意图;
(2)设计例题l的简要教学过程,并给出解题后的小结提纲;
(3)请设计例题2的变式题,以进-步理解和巩固定理。
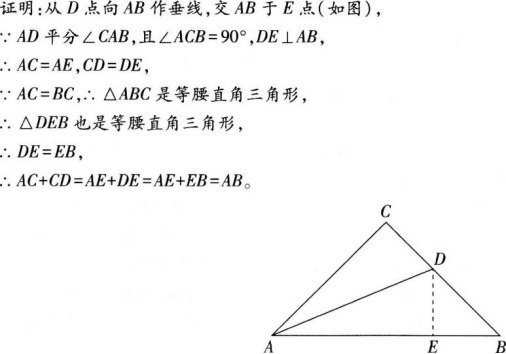
例题l的证明需要构造辅助线,即从D点向AB作垂线,交AB于E点,然后根据角平分线性质(角的平分线上的点到角的两边的距离相等)和题中条件得到CD=DE,AC=AE,再根据题中条件分析△DEB(等腰直角三角形),进而得到DE=EB,从而可证得AC+CD=AE+DE=AE+EB=AB。因此,在练习过程中可以进一步使学生理解角平分线的性质定理,学会利用角平分线的性质解决问题,顺利达成①和②的教学目标。同时根据找到的相等的线段,将要求证明的等式AC+CD=AB进行转化,可以进一步提高学生利用转化的数学思想毹决问题的能力,辅助线技巧的引入,有助于开拓学生的思维方式,丰富学生掌握的数学解题方法。
例题2的设计意图
例题2是一个实际应用题,问题的解决需要学生深刻理解角平分线的性质并会把该数学性质与实际问题联系在一起,懂得将实际问题抽象到一般的数学模型,这进一步加深了学生对角平分线性质的认识,并利用该性质解决实际问题,能够达成①和②的教学目标。问题的解决需要学生用尺规作图法解答,从而顺利达成③的教学目标。
(2)教学过程
教师在多媒体上播放例题1中的图片,先给予学生一段时间自主思考,独立解答,教师巡查。若绝大多数学生能够顺利解答出答案,则教师挑选几个学生在黑板上写下自己的证明过程,并让其说出依据,教师给予一定的评价。若学生的解答有困难,则教师让学生分组讨论,集思广益,在交流合作中得出结果,同时教师通过设问的方式层层引导学生思考,降低习题的难度,如可以提出问题。
问题l:由∠ACB=90。,AD平分∠CAB可以得到什么结论?(CD的长度表示的是∠CAB平分线上一点D到边AC的距离)
教师将BD擦去,让学生观察。
问题2:由问题l可知CD的长度表示的是D点到边AC的距离,根据角平分线性质,思考一下D点到∠CAB另一边AB的距离怎么表示呢?(引导学生作辅助线)
问题3:根据所作的辅助线,可以得到哪些相等的线段?(AC=AE,CD=伽,所以AC+CD=AE+DE)
问题4:想想还有什么条件没用,△ABC和ADEB是特殊三角形吗?
学生经过教师的启发,自主思考解答,当大多数学生得出正确结论后,教师随机让学生谈一谈解答步骤、思考过程以及之前思考时的误区,总结心得,教师给予积极评价。最后,教师可以在多媒体或黑板上给出证明过程。
小结提纲l:题中给出角平分线条件时,要思考角平分线带来的隐含条件,如最基本的平分出两个相等的角,角平分线上的点到角的两边的距离相等。要学会挖掘题设的隐含条件,这就需要我们扎实地掌握基础知识,能够做到举一反三。
小结提纲2:当直接解答困难时,可以适当地添加辅助线,将问题转化为容易求解或证明的形式。辅助线的添加需要对题目有深刻的认识以及对相关基础知识的牢固把握,所以需要重视对基础知识的学习并且要做有针对性的练习。
小结提纲3:知识之间有着多种关联性,题目的考察也不可能只涉及一个知识点(如本题不仅涉及角平分线性质的考察,还涉及等腰直角三角形性质的知识),这就要求我们要融会贯通,合理地利用已学知识,具体分析求解。
(3)设计变式题如下:
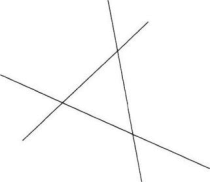
如图,直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有几处?作图画出可能的地址。
你可能感兴趣的试题
A.36
B.48
C.72
D.78
A.1/2
B.2
C.4
D.1/4
最新试题
已知向量m=(sinx,cosx),n=(cosx,cosx),f(x)=m*n, (1)求函数f(x)的最小正周期:
(10分)已知数列{an}满足a1=3,an+1= an +2n, (1)求{ an }的通项公式an; (2)若b
“星光大道”民间歌手选拨现场有数百观众和5名参赛选手,5名参赛选手代号分别为1至5号。现场观众根据自己的喜好投票,选出最
已知|a|=1,|b|=2。 (1)若a∥b,求a·b; (2)若a,b的夹角为60°,求|a+b|; (3)若
分别用分析法,综合法证明如下命题。 命题:如图。三角形ABC的角B和角C的角平分线相交于点O,过点O作平行于底边BC的
设函数f(X)=X+aln(1+X)+bXsinX,g(X)=kX3,若f(X)与g(X)在X→0是等价无穷小,求a,b
如图,正方体ABCD-A1B1C1D1中,求BB1与平面C1DB所成角的正切值为__________。
若实数x,Y满足则z的取值范围是_________。
两个袋子中都装有红、黄、白三个小球,这些球除颜色外,形状、大小、质地等完全相同。搅匀后,在看不到球的条件下,随机分别从两