中国建设银行
从l,2,3…n中,任取57个数,使这57个数必有两个数的差为l3,则n的最大值为
多少?
A.106
B.107
C.108
D.109
根据两数之差不能为13.构造(1,14,27,40,..)、(2,15,28,41,…)、(3,16,29,42.…)、(13.26.39,…)。显然,每个括号中均不能取连续的两个数,现要求任取57个数必有两数差为l3时,n的最大值.那考虑取57个可能没有两数之差为l3时,n的最小值,显然每组数中取第1,3,5,7,…个数可使n最小,相当于每26个数取前l3个数,那么要取57个数,57÷13=4…5,n最小为26×4+5=109,即n为109时就能满足取57个数且可能没有两数之差为l3的情况,当n为108时,必然有两个数之差为l3,所以n的最大值为108,应选择C.
你可能感兴趣的试题
一项工程由甲、乙两队合作30天可以完成。若甲单独做24天后乙队加入,两队合作l0天后,甲队被调走,乙队继续做了l7天才能完成,则这项工程由甲、乙两队单独完成各需多少天?
A.52、70.5
B.52.5、70
C.70、52.5
D.70.5、52
如图,有一个边长为20厘米的大正方体,分别在它的角上、棱上、面上各挖掉一个大小相同的小立方体后,表面积变为2454平方厘米,那么挖掉的小立方体的边长是多少厘米?
A.2
B.2.5
C.3
D.3.5
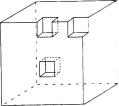
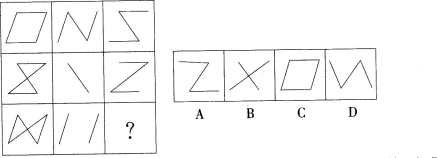
A.如图
B.如上图
C.如图所示
D.如上图所示
最新试题
As used in the first line of the second paragraph, the wor
This passage implies that( ).
We can infer from the passage that( ).
According to the passage, special cases refer to cases whe
根据下面内容,回答题 You're busy filling out the application form f
Which of the following would be the best title for text?
On which of the following would the author most probably a
The reasons why young worker will be harder to recruit exc
In Paragraph 5, the author discusses that ( ).
根据下面内容,回答题 Rising wages-together with currency fluctuatio
